Lesson 11: Putting It All Together
- Summary
- *
- Text version
- *
- Exercises
- *
- Download source
Overview
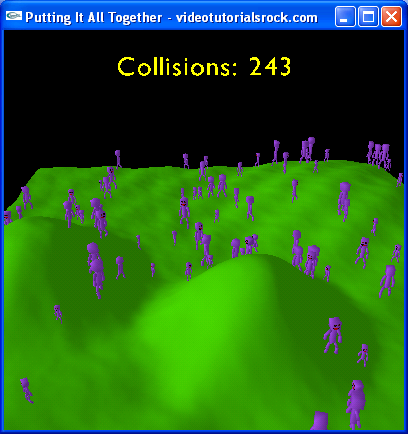
If you haven't skipped anything, you've just learned about terrain, drawing text, animation, and collision detection. We're going to look at a program that uses all of these topics, in order to crystallize what we've learned. Our program features a bunch of blocky looking guys running around and bouncing off of each other, as shown below:
The Code
Let's just dive right into some code.
const float PI = 3.1415926535f; const int NUM_GUYS = 100; //The width of the terrain in units, after scaling const float TERRAIN_WIDTH = 50.0f; //The amount of time between each time that we handle collisions const float TIME_BETWEEN_HANDLE_COLLISIONS = 0.01f;
We start with some constants, beginning with the constant PI. I have no idea what this constant was supposed to be when I wrote it. I know that pi is some kind of Greek letter, but where the heck did I come up with 3.14159? If I'd spelled it "PIE", then it might make a little sense. As it is, this constant is just a mystery to me.
Next, we have the number of guys that are running around on the terrain. We have a constant indicating the width of the terrain, after scaling it. There's also a constant indicating the amount of time between handling collisions. As in the lesson on collision detection, we'll alternate between advancing all of the guys by some amount of time and handling all of the collisions betweeen guys. So TIME_BETWEEN_HANDLE_COLLISIONS is the number of seconds by which we advance the guys between handling collisions.
//Returns a random float from 0 to < 1 float randomFloat() { return (float)rand() / ((float)RAND_MAX + 1); }
This function returns a random value from 0 to 1.
//Represents a terrain, by storing a set of heights and normals at 2D locations class Terrain { //... }; //Loads a terrain from a heightmap. The heights of the terrain range from //-height / 2 to height / 2. Terrain* loadTerrain(const char* filename, float height) { //... }
Now we have our Terrain class and the loadTerrain function, which are exactly the same as in the lesson on terrains.
//Returns the approximate height of the terrain at the specified (x, z) position float heightAt(Terrain* terrain, float x, float z) {
We have a new function called heightAt, which determines the height of a terrain at a particular fractional (x, z) coordinate. We'll do this by taking a weighted average of the four heights of the grid points for the grid cell in which the point lies. This is a little different from the height indicated by the way we draw terrains; if you remember, we broke up each grid cell into two triangles when drawing them. But if the terrain is sufficiently smooth, it shouldn't matter very much. Anyway, I think that the weighted average approach gives a more appropriate height.
//Make (x, z) lie within the bounds of the terrain if (x < 0) { x = 0; } else if (x > terrain->width() - 1) { x = terrain->width() - 1; } if (z < 0) { z = 0; } else if (z > terrain->length() - 1) { z = terrain->length() - 1; }
First, the function makes sure that (x, z) lies within the bounds of the terrain.
//Compute the grid cell in which (x, z) lies and how close we are to the //left and outward edges int leftX = (int)x; if (leftX == terrain->width() - 1) { leftX--; } float fracX = x - leftX; int outZ = (int)z; if (outZ == terrain->width() - 1) { outZ--; } float fracZ = z - outZ;
Next, heightAt computes leftX and outZ, which indicate the grid cell in which (x, z) lies, and fracX and fracZ, the distance from (leftX, outZ).
//Compute the four heights for the grid cell float h11 = terrain->getHeight(leftX, outZ); float h12 = terrain->getHeight(leftX, outZ + 1); float h21 = terrain->getHeight(leftX + 1, outZ); float h22 = terrain->getHeight(leftX + 1, outZ + 1); //Take a weighted average of the four heights return (1 - fracX) * ((1 - fracZ) * h11 + fracZ * h12) + fracX * ((1 - fracZ) * h21 + fracZ * h22); }
We determine the four heights of the grid cell in which (x, z) lies and return a weighted average of them.
//The amount by which the Guy class's step function advances the state of a guy const float GUY_STEP_TIME = 0.01f;
Each block guy will keep track of some information about itself. They'll have their own advance and step methods. The state of each guy will be updated over small intervals of time, each interval having a duration of GUY_STEP_TIME seconds.
//Represents a guy class Guy { private: MD2Model* model; Terrain* terrain;
Here's our Guy class, which keeps track of all information regarding a single block guy. Each guy stores the terrain on which he's walking and the model for a guy.
float terrainScale; //The scaling factor for the terrain float x0; float z0;
Each guy stores a scaling factor for the terrain, the amount by which it is scaled so that it is TERRAIN_WIDTH units wide. They also keep track of their positions.
float animTime; //The current position in the animation of the model
Each guy has a field indicating its position in the current animation. If you remember from the lesson on animation, our MD2Model class had an advance method indicating the current position in the animation. However, in this program, each guy will be at a different position in the animation. For this program, I've altered the MD2Model class by removing the advance method, and by changing the draw method to take as a parameter the animation time.
float radius0; //The approximate radius of the guy
The radius0 field indicates the approximate radius of a guy. This number will be used to determine the amount by which to scale the guy when we draw him. It'll also be used for collision detection; we'll approximate each guy as a cylinder for the purposes of collision detection.
float speed; //The angle at which the guy is currently walking, in radians. An angle //of 0 indicates the positive x direction, while an angle of PI / 2 //indicates the positive z direction. The angle always lies between 0 //and 2 * PI. float angle; //The amount of time until step() should next be called float timeUntilNextStep;
We have a few more fields here. speed indicates the speed of the guy in units per second. angle indicates the direction in which the guy is walking, such that 0 indicates the positive x direction and PI / 2 indicates the positive z direction. This is the way that angles are frequently represented in the x-y plane (although technically we're concerned with the x-z plane). timeUntilNextStep is the amount of time until we next call step().
bool isTurningLeft; //Whether the guy is currently turning left float timeUntilSwitchDir; //The amount of time until switching direction
Each guy is turning either left or right while he walks. isTurningLeft indicates the direction that a guy is currently turning. Every so often, each guy will change directions; timeUntilSwitchDir is the amount of time in which a guy will switch.
//Advances the state of the guy by GUY_STEP_TIME seconds (without //altering animTime) void step() { //Update the turning direction information timeUntilSwitchDir -= GUY_STEP_TIME; while (timeUntilSwitchDir <= 0) { timeUntilSwitchDir += 20 * randomFloat() + 15; isTurningLeft = !isTurningLeft; }
Here's the step method for guys. First, we take care of updating information regarding the direction the guy is turning.
//Update the position and angle float maxX = terrainScale * (terrain->width() - 1) - radius0; float maxZ = terrainScale * (terrain->length() - 1) - radius0;
We compute maxX and maxZ, which indicate the farthest the guy can be in the positive x and z directions.
x0 += velocityX() * GUY_STEP_TIME;
z0 += velocityZ() * GUY_STEP_TIME;We increase the x0 and z0 fields to move the guy forward. The velocityX() and velocityZ methods, which we'll see later, give us the velocity of the guy based on his speed and the direction he is walking.
bool hitEdge = false; if (x0 < radius0) { x0 = radius0; hitEdge = true; } else if (x0 > maxX) { x0 = maxX; hitEdge = true; } if (z0 < radius0) { z0 = radius0; hitEdge = true; } else if (z0 > maxZ) { z0 = maxZ; hitEdge = true; }
If the guy has now exceeded an edge of the map, we move his to the exact edge of the map and set the hitEdge variable to true.
if (hitEdge) { //Turn more quickly if we've hit the edge if (isTurningLeft) { angle -= 0.5f * speed * GUY_STEP_TIME; } else { angle += 0.5f * speed * GUY_STEP_TIME; } } else if (isTurningLeft) { angle -= 0.05f * speed * GUY_STEP_TIME; } else { angle += 0.05f * speed * GUY_STEP_TIME; }
This code makes the guy turn, by adjusting the angle variable. If the guy is at the edge of the terrain, he turns more quickly, so that he doesn't face the edge of the terrain for very long.
while (angle > 2 * PI) { angle -= 2 * PI; } while (angle < 0) { angle += 2 * PI; } }
These two while loops ensure that angle lies between 0 and 2 * PI.
public: Guy(MD2Model* model1, Terrain* terrain1, float terrainScale1) { model = model1; terrain = terrain1; terrainScale = terrainScale1; animTime = 0; timeUntilNextStep = 0; //Initialize certain fields to random values radius0 = 0.4f * randomFloat() + 0.25f; x0 = randomFloat() * (terrainScale * (terrain->width() - 1) - radius0) + radius0; z0 = randomFloat() * (terrainScale * (terrain->length() - 1) - radius0) + radius0; speed = 1.5f * randomFloat() + 2.0f; isTurningLeft = randomFloat() < 0.5f; angle = 2 * PI * randomFloat(); timeUntilSwitchDir = randomFloat() * (20 * randomFloat() + 15); }
The constructor for the Guy class just initializes some variables, some of which are set to random values.
//Advances the state of the guy by the specified amount of time, by //calling step() the appropriate number of times and adjusting animTime void advance(float dt) { //Adjust animTime animTime += 0.45f * dt * speed / radius0; if (animTime > -100000000 && animTime < 1000000000) { animTime -= (int)animTime; if (animTime < 0) { animTime += 1; } } else { animTime = 0; } //Call step() the appropriate number of times while (dt > 0) { if (timeUntilNextStep < dt) { dt -= timeUntilNextStep; step(); timeUntilNextStep = GUY_STEP_TIME; } else { timeUntilNextStep -= dt; dt = 0; } } }
The advance() method advances the state of a guy by a given amount of time. It just changes animTime and calls step() the appropriate number of times.
void draw() { if (model == NULL) { return; } float scale = radius0 / 2.5f; glPushMatrix(); glTranslatef(x0, scale * 10.0f + y(), z0); glRotatef(90 - angle * 180 / PI, 0, 1, 0); glColor3f(1, 1, 1); glRotatef(180.0f, 0.0f, 1.0f, 0.0f); glRotatef(-90.0f, 0.0f, 0.0f, 1.0f); glScalef(scale, scale, scale); model->draw(animTime); glPopMatrix(); }
This method takes care of drawing one of our blocky friends. If the model is NULL, we don't draw anything. Otherwise, we translate, rotate, and scale, and then call draw on the model. The scaling factor is proportional to the radius of the guy. The translation moves to the location of the guy. It calls the y() method that we'll see later, which uses heightAt to find out the height of the terrain at the guy's position. You'll notice that we're moving a little above y(), since we need to move above the surface of the terrain to the center of the guy.
After translating, we rotate by 90 - angle * 180 / PI, in order to have the guy face the direction that he's walking. We have to take 90 minus the angle for it to work. This is because a rotation of 0 would have the guy walking in the positive z direction, whereas an angle of 0 indicates that the guy is walking in the positive x direction. So basically, this converts from the angle variable to the amount of rotation that we need.
We set the color to white, so that we don't have any kind of weird coloring applied to the model. We do a couple of rotations that make it so that the model, which I oriented the wrong way when I made him in Blender, is oriented correctly.
float x() { return x0; } float z() { return z0; }
We have methods for returning the position of a guy.
//Returns the current height of the guy on the terrain float y() { return terrainScale * heightAt(terrain, x0 / terrainScale, z0 / terrainScale); }
The y() method uses the heightAt function to figure out the vertical position of the guy.
float velocityX() { return speed * cos(angle); } float velocityZ() { return speed * sin(angle); }
These methods tell us the velocity of the guy in the x and z directions.
//Returns the approximate radius of the guy float radius() { return radius0; } //Returns the angle at which the guy is currently walking, in radians. //An angle of 0 indicates the positive x direction, while an angle of //PI / 2 indicates the positive z direction. float walkAngle() { return angle; }
These methods return the radius and angle of a guy.
//Adjusts the angle at which this guy is walking in response to a //collision with the specified guy void bounceOff(Guy* otherGuy) { float vx = velocityX(); float vz = velocityZ(); float dx = otherGuy->x0 - x0; float dz = otherGuy->z0 - z0; float m = sqrt(dx * dx + dz * dz); dx /= m; dz /= m; float dotProduct = vx * dx + vz * dz; vx -= 2 * dotProduct * dx; vz -= 2 * dotProduct * dz; if (vx != 0 || vz != 0) { angle = atan2(vz, vx); } } };
The bounceOff method is used for handling collisions. It makes the guy change direction so that he bounces of another guy. It operates similarly to the bouncing in the program on collision detection, but works in two dimensions. It computes the direction from the first guy to the other guy, takes the dot product of that vector and the velocity vector, and subtracts twice the dot product times the direction from the velocity. It uses the resultant vector to determine the new angle in which the guy will walk, using the atan2 C function. atan2 just returns the angle of a vector, where the first parameter is the y component of the vector and the second parameter is the x component of the vector.
Collision Detection Code
Next, we have a bunch of code related to collision detection.
struct GuyPair {
Guy* guy1;
Guy* guy2;
};We have a GuyPair function which stores potential collisions.
const int MAX_QUADTREE_DEPTH = 6; const int MIN_GUYS_PER_QUADTREE = 2; const int MAX_GUYS_PER_QUADTREE = 5;
For this program, we're using a quadtree for collision detection, the two-dimensional analog of the octree we used in the program with all of the bouncing balls. We have some parameters for the quadtree indicating when to divide or un-divide a particular quadtree node.
//Our data structure for making collision detection faster class Quadtree { private: float minX; float minZ; float maxX; float maxZ; float centerX; //(minX + maxX) / 2 float centerZ; //(minZ + maxZ) / 2
We've been through octrees before, but let's run though our Quadtree class to make sure that we still understand how everything works. We have the minX, minZ, maxX, and maxZ fields, which indicate the rectangle for a given node, and centerX and centerZ, the coordinates of the center of that rectangle.
/* The children of this, if this has any. children[0][*] are the * children with x coordinates ranging from minX to centerX. * children[1][*] are the children with x coordinates ranging from * centerX to maxX. Similarly for the other dimension of the children * array. */ Quadtree *children[2][2]; //Whether this has children bool hasChildren; //The guys in this, if this doesn't have any children set<Guy*> guys; //The depth of this in the tree int depth; //The number of guys in this, including those stored in its children int numGuys;
We have the children field, which is a two-dimensional array of Quadtree objects storing the children of a node, if there are any. The hasChildren field tells us whether a quadtree node has any children. The guys set stores all of the guys in a node, if the node has no children. depth indicates the depth of a node in the quadtree. numGuys is the number of guys in a node or any of its children.
//Adds a guy to or removes one from the children of this void fileGuy(Guy* guy, float x, float z, bool addGuy) { //Figure out in which child(ren) the guy belongs for(int xi = 0; xi < 2; xi++) { if (xi == 0) { if (x - guy->radius() > centerX) { continue; } } else if (x + guy->radius() < centerX) { continue; } for(int zi = 0; zi < 2; zi++) { if (zi == 0) { if (z - guy->radius() > centerZ) { continue; } } else if (z + guy->radius() < centerZ) { continue; } //Add or remove the guy if (addGuy) { children[xi][zi]->add(guy); } else { children[xi][zi]->remove(guy, x, z); } } } }
fileGuy figures out in which of the children a particular guy belongs and either adds the guy to or removes the guy from these children, depending on whether addGuy is true.
//Creates children of this, and moves the guys in this to the children void haveChildren() { for(int x = 0; x < 2; x++) { float minX2; float maxX2; if (x == 0) { minX2 = minX; maxX2 = centerX; } else { minX2 = centerX; maxX2 = maxX; } for(int z = 0; z < 2; z++) { float minZ2; float maxZ2; if (z == 0) { minZ2 = minZ; maxZ2 = centerZ; } else { minZ2 = centerZ; maxZ2 = maxZ; } children[x][z] = new Quadtree(minX2, maxX2, minZ2, maxZ2, depth + 1); } } //Remove all guys from "guys" and add them to the new children for(set<Guy*>::iterator it = guys.begin(); it != guys.end(); it++) { Guy* guy = *it; fileGuy(guy, guy->x(), guy->z(), true); } guys.clear(); hasChildren = true; }
The haveChildren method divides a quadtree node, placing all of the guys into four new child nodes.
//Adds all guys in this or one of its descendants to the specified set void collectGuys(set<Guy*> &gs) { if (hasChildren) { for(int x = 0; x < 2; x++) { for(int z = 0; z < 2; z++) { children[x][z]->collectGuys(gs); } } } else { for(set<Guy*>::iterator it = guys.begin(); it != guys.end(); it++) { Guy* guy = *it; gs.insert(guy); } } }
The collectGuys method puts all of the guys in a particular node or any of its children into a given set.
//Destroys the children of this, and moves all guys in its descendants //to the "guys" set void destroyChildren() { //Move all guys in descendants of this to the "guys" set collectGuys(guys); for(int x = 0; x < 2; x++) { for(int z = 0; z < 2; z++) { delete children[x][z]; } } hasChildren = false; }
The destroyChildren method un-divides a quadtree node by collecting all of the guys in its children into the guys set and deleting the children.
//Removes the specified guy at the indicated position void remove(Guy* guy, float x, float z) { numGuys--; if (hasChildren && numGuys < MIN_GUYS_PER_QUADTREE) { destroyChildren(); } if (hasChildren) { fileGuy(guy, x, z, false); } else { guys.erase(guy); } }
The remove method removes a guy at a particular position from a node. It calls destroyChildren if the node has few children. It then either uses fileGuy to remove the guy from its children or just removes the guy from the guys set.
public: //Constructs a new Quadtree. d is the depth, which starts at 1. Quadtree(float minX1, float minZ1, float maxX1, float maxZ1, int d) { minX = minX1; minZ = minZ1; maxX = maxX1; maxZ = maxZ1; centerX = (minX + maxX) / 2; centerZ = (minZ + maxZ) / 2; depth = d; numGuys = 0; hasChildren = false; }
We have our constructor, which initializes some of the fields.
~Quadtree() {
if (hasChildren) {
destroyChildren();
}
}The destructor deletes the children if there are any.
//Adds a guy to this void add(Guy* guy) { numGuys++; if (!hasChildren && depth < MAX_QUADTREE_DEPTH && numGuys > MAX_GUYS_PER_QUADTREE) { haveChildren(); } if (hasChildren) { fileGuy(guy, guy->x(), guy->z(), true); } else { guys.insert(guy); } }
The add method divides the quadree node if there are too many children. It then either uses fileGuy to put the guy into the appropriate children, or it adds the guy to the guys set.
//Removes a guy from this void remove(Guy* guy) { remove(guy, guy->x(), guy->z()); }
This remove method calls the other remove method to remove a guy from his current position.
//Changes the position of a guy in this from the specified position to //its current position void guyMoved(Guy* guy, float x, float z) { remove(guy, x, z); add(guy); }
The guyMoved method is called whenever a guy's position changes. It operates by removing the guy at his old position and then adding him again.
//Adds potential collisions to the specified set void potentialCollisions(vector<GuyPair> &collisions) { if (hasChildren) { for(int x = 0; x < 2; x++) { for(int z = 0; z < 2; z++) { children[x][z]->potentialCollisions(collisions); } } } else { //Add all pairs (guy1, guy2) from guys for(set<Guy*>::iterator it = guys.begin(); it != guys.end(); it++) { Guy* guy1 = *it; for(set<Guy*>::iterator it2 = guys.begin(); it2 != guys.end(); it2++) { Guy* guy2 = *it2; //This test makes sure that we only add each pair once if (guy1 < guy2) { GuyPair gp; gp.guy1 = guy1; gp.guy2 = guy2; collisions.push_back(gp); } } } } } };
The potentialCollisions method figures out possible collisions between pairs of guys. It recurses on the children if there are any and takes every pair of guys otherwise.
void potentialCollisions(vector<GuyPair> &cs, Quadtree* quadtree) {
quadtree->potentialCollisions(cs);
}The potentialCollisions function just calls the quadtree's potentialCollisions method.
//Returns whether guy1 and guy2 are currently colliding bool testCollision(Guy* guy1, Guy* guy2) { float dx = guy1->x() - guy2->x(); float dz = guy1->z() - guy2->z(); float r = guy1->radius() + guy2->radius(); if (dx * dx + dz * dz < r * r) { float vx = guy1->velocityX() - guy2->velocityX(); float vz = guy1->velocityZ() - guy2->velocityZ(); return vx * dx + vz * dz < 0; } else { return false; } }
testCollision determines whether there actually is a collision between two particular guys. A collision occurs when the distance between the guys is less than the sum of their radii, and the guys are currently moving towards each other.
void handleCollisions(vector<Guy*> &guys, Quadtree* quadtree, int &numCollisions) { vector<GuyPair> gps; potentialCollisions(gps, quadtree); for(unsigned int i = 0; i < gps.size(); i++) { GuyPair gp = gps[i]; Guy* g1 = gp.guy1; Guy* g2 = gp.guy2; if (testCollision(g1, g2)) { g1->bounceOff(g2); g2->bounceOff(g1); numCollisions++; } } }
The handleCollisions function goes through potential collisions and finds the ones that are actually collisions. For each collision, it makes the guys bounce off of each other using the bounceOff method, and increments a numCollisions variable, which stores the total number of collisions that have occurred. If you remember from the screenshot at the beginning, we'll be displaying the total number of collisions, so we need to keep track of this amount.
The Rest of the Code
//Moves the guys over the given interval of time, without handling collisions void moveGuys(vector<Guy*> &guys, Quadtree* quadtree, float dt) { for(unsigned int i = 0; i < guys.size(); i++) { Guy* guy = guys[i]; float oldX = guy->x(); float oldZ = guy->z(); guy->advance(dt); quadtree->guyMoved(guy, oldX, oldZ); } }
This function takes care of moving the guys over a certain interval of time, by calling advance on the guys and calling guyMoved on the quadtree for each guy.
//Advances the state of the guys over the indicated interval of time void advance(vector<Guy*> &guys, Quadtree* quadtree, float t, float &timeUntilHandleCollisions, int &numCollisions) { while (t > 0) { if (timeUntilHandleCollisions <= t) { moveGuys(guys, quadtree, timeUntilHandleCollisions); handleCollisions(guys, quadtree, numCollisions); t -= timeUntilHandleCollisions; timeUntilHandleCollisions = TIME_BETWEEN_HANDLE_COLLISIONS; } else { moveGuys(guys, quadtree, t); timeUntilHandleCollisions -= t; t = 0; } } }
The advance function moves the guys over a certain interval of time, by alternately using moveGuys to advance the guys an interval of TIME_BETWEEN_HANDLE_COLLISIONS and calling handleCollisions.
//Returns a vector of numGuys new guys vector<Guy*> makeGuys(int numGuys, MD2Model* model, Terrain* terrain) { vector<Guy*> guys; for(int i = 0; i < numGuys; i++) { guys.push_back(new Guy(model, terrain, TERRAIN_WIDTH / (terrain->width() - 1))); } return guys; }
makeGuys constructs and returns numGuys new guys.
//Draws the terrain void drawTerrain(Terrain* terrain) glDisable(GL_TEXTURE_2D); glColor3f(0.3f, 0.9f, 0.0f); for(int z = 0; z < terrain->length() - 1; z++) { glBegin(GL_TRIANGLE_STRIP); for(int x = 0; x < terrain->width(); x++) { Vec3f normal = terrain->getNormal(x, z); glNormal3f(normal[0], normal[1], normal[2]); glVertex3f(x, terrain->getHeight(x, z), z); normal = terrain->getNormal(x, z + 1); glNormal3f(normal[0], normal[1], normal[2]); glVertex3f(x, terrain->getHeight(x, z + 1), z + 1); } glEnd(); } }
The drawTerrain function takes care of drawing the terrain. The code is the same as the code from the lesson on terrains, although if you remember in the terrain lesson, this code was in the drawScene function.
//Draws a string at the top of the screen indicating that the specified number //of collisions have occurred void drawNumCollisions(int numCollisions) { ostringstream oss; oss << "Collisions: " << numCollisions; string str = oss.str();
The drawNumCollisions function will take care of drawing the total number of collisions at the top of the screen. First of all, we'll use string streams to get a string that reads "Collisions: 500", or whatever the number of collisions happens to be. We used #include <sstream> at the top of main.cpp to include string streams. You can use the << operator to add to the end of an ostringstream. So, we add "Collisions: " to the end of a new string stream, followed by numCollisions. Now, the string stream has what we want. To get a string containing its contents, we call str() on the stream. This method returns a C++ string object rather than a character array, a C-style string. C++ strings behave a lot like character arrays; in fact, you can access the character array for a string object by calling c_str().
glDisable(GL_TEXTURE_2D);
glDisable(GL_LIGHTING);
glColor3f(1.0f, 1.0f, 0.0f);
glPushMatrix();
glTranslatef(0.0f, 1.7f, -5.0f);
glScalef(0.2f, 0.2f, 0.2f);
t3dDraw2D(str, 0, 0);
glPopMatrix();
glEnable(GL_LIGHTING);
}Now we do our OpenGL thing, translating, coloring, pushing and popping, all that business. We have a call to t3dDraw2D to actually draw the string, which we will have center-aligned both horizontally and vertically.
MD2Model* _model; vector<Guy*> _guys; Terrain* _terrain; float _angle = 0; Quadtree* _quadtree; //The amount of time until we next check for and handle all collisions float _timeUntilHandleCollisions = 0; int _numCollisions; //The total number of collisions that have occurred
As usual, we have a bunch of variables, which are mostly self-explanatory. _angle is the camera angle, and _timeUntilHandleCollisions is the amount of time until we'll next handle collisions.
void cleanup() { delete _model; for(unsigned int i = 0; i < _guys.size(); i++) { delete _guys[i]; } t3dCleanup(); }
The cleanup function deletes the model and the Guy objects, and calls t3dCleanup() to tell the text drawing functionality to dispose of its resources.
void initRendering() { //... t3dInit(); //Initialize text drawing functionality //Load the model _model = MD2Model::load("blockybalboa.md2"); if (_model != NULL) { _model->setAnimation("run"); } }
In initRendering, we call t3dInit to set up the text drawing functionality. We load the model (which I created in Blender). The model file is named blockybalboa.md2, as our block guys are named Blocky Balboa. Then, we switch to the running animation.
void drawScene() { //... //Draw the number of collisions that have occurred drawNumCollisions(_numCollisions); //The scaling factor for the terrain float scale = TERRAIN_WIDTH / (_terrain->width() - 1); //... //Draw the guys for(unsigned int i = 0; i < _guys.size(); i++) { _guys[i]->draw(); } //Draw the terrain glScalef(scale, scale, scale); drawTerrain(_terrain); //... }
The drawScene function for the most part calls drawNumCollisions, the Guy class's draw method, and the drawTerrain function.
void update(int value) { _angle += 0.3f; if (_angle > 360) { _angle -= 360; } advance(_guys, _quadtree, 0.025f, _timeUntilHandleCollisions, _numCollisions); //... }
update increases the camera angle and calls advance to advance the positions of the guys.
int main(int argc, char** argv) { //... _terrain = loadTerrain("heightmap.bmp", 30.0f); //Load the terrain _guys = makeGuys(NUM_GUYS, _model, _terrain); //Create the guys //Compute the scaling factor for the terrain float scaledTerrainLength = TERRAIN_WIDTH / (_terrain->width() - 1) * (_terrain->length() - 1); //Construct and initialize the quadtree _quadtree = new Quadtree(0, 0, TERRAIN_WIDTH, scaledTerrainLength, 1); for(unsigned int i = 0; i < _guys.size(); i++) { _quadtree->add(_guys[i]); } //... }
The main function takes care of loading the terrain, creating all of the guys, and setting up the quadtree.
So that's pretty much a run down of the program. Hopefully, all this jaberring has helped solidify what you learned in the last few lessons.
Next is "Part 3: Special Effects".
- Summary
- *
- Text version
- *
- Exercises
- *
- Download source