Lesson 10: Collision Detection
- Summary
- *
- Text version
- *
- Exercises
- *
- Download source
Be forwarned: this lesson will be fairly complex.
The Problem of Collision Detection
A common thing to do in video games, simulations, and other programs is to have something happen when two objects hit each other, such as having them bounce off each other or stop. For this, we need to use collision detection. The basic idea of collision detection is to locate which objects are intersecting at any given moment, so that we can handle the intersection in some way. Often, we want to do this in real-time, so our solution had better be fast.
It turns out that collision detection is hard. For this reason, in a lot of demo or test versions of upcoming games, the collision detection is rather buggy.
Furthermore, there's no one right answer for collision detection. It all depends on what program you are making. Important factors for designing collision detection include when and how collisions "usually" occur, what types of flaws are more or less noticeable to the user, and which collisions matter the most. In particular, if only collisions with the protagonist really matter, collision detection is a much different problem than if all collisions between a pair of game objects are relevant.
I can only cover a fraction of techniques used in collision detection. Frequently, collision detection revolves around tricks that group together closer objects. Often, it utilizes the fact that the scene doesn't change much between frames. You can get exact collision detection based on all of the 3D polygons of the objects, but usually it's better to approximate the shapes of objects as one or more simpler shapes such as boxes, cylinders, and spheres. Another common technique is to have a quick and dirty check that determines whether two objects might be colliding, which one performs before potentially wasting time on a longer check. For example, one could check whether the bounding spheres of two objects intersect before performing a more complicated check.
Our Problem
Of the many collision detection techniques, I will teach you only one in detail, to give you an idea of possible collision detection strategies. First, let's look at the problem we want to solve. Download, compile, and run the program. We have a box with the upper and lower walls shown; the rest of the walls are invisible. Every time you press the space bar, it will randomly add 20 balls to the box. They fall with gravity and bounce off of each other and the walls.

The basic idea of the program is to step by 10 milliseconds, updating the balls' positions and velocities, check for collisions and make all colliding balls bounce, and repeat. We're going to focus on the part where we check for collisions.
To find all of the collisions, one thing we could do is check every pair of balls, and see if their distances are less than the sum of their radii. However, by the time we reached 300 balls, we'd have to check about 50,000 pairs of balls for potential collisions, even though there are usually very few collisions. Maybe there's a faster way.
One thing we could try is to divide the cube in half along each dimension, into eight smaller cubes. Then, we could figure out in which cube(s) each ball is, and check every pair of balls in each smaller cube for collisions. Take a look at this diagram of the 2D equivalent of this technique:
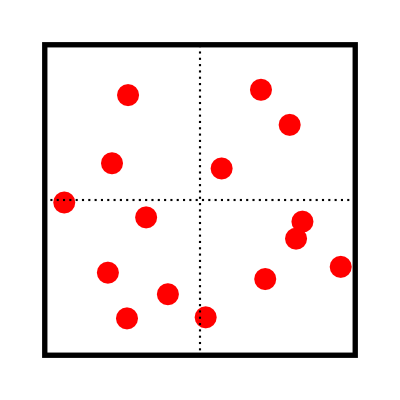
If we were to check every pair of balls in the above picture for collisions, we would have to check 105 pairs of balls. If instead, we check each pair of balls in each of the four smaller squares, there are only 3 + 3 + 15 + 10 = 31 pairs to check.
Note that two of the balls appear in two of the smaller squares. This will also occur in the 3D version of the problem, but it will be relatively uncommon.
We've sped things up a little, but we can do even better. Our basic strategy to find potential collisions in a cube was to divide the cube into eight smaller cubes, and then give some set of potential collisions within each smaller cube. For these potential collisions, we took every pair of balls in each smaller cube. But why stop there? We can divide the smaller cubes themselves into eight cubes, and take every pair of balls in each even smaller cube, so that we have even fewer pairs of balls to check.
We can repeat this indefinitely, but after a while, it ceases to be helpful. For instance, if there are very few balls in a cube, say 3, then it's easier to just check all of the pairs of balls than to keep dividing up the cube. Plus, the more we divide up the cubes, the more frequently balls will appear in multiple cubes, which is bad, because this tends to produce duplicate pairs and false positives. So, let's use the following strategy: for a given cube, if there are a lot of balls in it, make eight smaller cubes, and let them take care of finding potential collisions. If there are not so many balls, just use every pair of balls as the set of potential collisions. This results in a tree structure; each cube is a node in the tree, and if it is divided into smaller cubes, these cubes are its eight children. It's called an "octree", with one "t" (the 2D equivalent is called a "quadtree"). Below is an example of the 2D version of the tree structure:
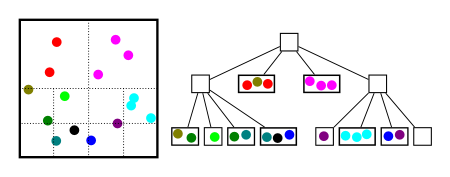
By further dividing the squares, we've reduced the number of pairs of balls to check even further, from 31 to 15.
Once the length of the cubes approaches the radius of the balls, subdividing the cubes will make it very common for the balls to appear in many cubes, which is bad. For this reason, we'll limit the depth of the tree. That is, if we were going to subdivide a cube, but the cube is already at some depth x in the tree, then we don't subdivide it.
Another thing: the scene doesn't change much from moment to moment. So, rather than constantly creating and destroying an octree, we'll create an octree at the beginning of the program, and whenever a ball moves or is created, we'll just change the octree. Now, not only do we need to divide up a cube when it has too many balls, but we have to un-divide a cube when it has too few, in order to ensure that each leaf-level cube has not too many, but not too few balls. So, whenever a cube goes above x balls, we'll divide it (unless the node is at the maximum allowable depth), and whenever a cube drops to below y balls, we'll un-divide it. We want x to be a little bigger than y, so that we don't have to keep dividing and un-dividing a given cube too frequently.
The Code for Basic Mechanics
Okay, let's take a look at some code. Be warned: the program is a good deal more complex than the programs in previous lessons. Before we look at the code for the octree, we'll look at the rest of the code.
After the include statements, we define the randomFloat function, which returns a random float from 0 to less than 1.
//Stores information regarding a ball struct Ball { Vec3f v; //Velocity Vec3f pos; //Position float r; //Radius Vec3f color; };
We define our ball structure, which has the velocity, position, radius, and color of each ball. The velocity of the ball indicates how quickly it is moving in each direction. For example, a velocity of (3, -2, -5) means that it is moving 3 units per second in the positive x direction, 2 units per second in the downward direction, and 5 units per second in the negative z direction.
enum Wall {WALL_LEFT, WALL_RIGHT, WALL_FAR, WALL_NEAR, WALL_TOP, WALL_BOTTOM};The six walls are represented in an enumeration.
//Stores a pair of balls struct BallPair { Ball* ball1; Ball* ball2; }; //Stores a ball and a wall struct BallWallPair { Ball* ball; Wall wall; };
We have structures to store ball-ball and ball-wall pairs, so that we can indicate potential collisions. Note that up until this point, I've been ignoring ball-wall collisions. This is because they take much less time to compute than ball-ball collisions, so it's not as important to optimize them. But don't worry, we'll get to them.
//Puts potential ball-ball collisions in potentialCollisions. It must return //all actual collisions, but it need not return only actual collisions. void potentialBallBallCollisions(vector<BallPair> &potentialCollisions, vector<Ball*> &balls, Octree* octree) { //Fast method octree->potentialBallBallCollisions(potentialCollisions); /* //Slow method for(unsigned int i = 0; i < balls.size(); i++) { for(unsigned int j = i + 1; j < balls.size(); j++) { BallPair bp; bp.ball1 = balls[i]; bp.ball2 = balls[j]; potentialCollisions.push_back(bp); } } */ } //Puts potential ball-wall collisions in potentialCollisions. It must return //all actual collisions, but it need not return only actual collisions. void potentialBallWallCollisions(vector<BallWallPair> &potentialCollisions, vector<Ball*> &balls, Octree* octree) { //Fast method octree->potentialBallWallCollisions(potentialCollisions); /* //Slow method Wall walls[] = {WALL_LEFT, WALL_RIGHT, WALL_FAR, WALL_NEAR, WALL_TOP, WALL_BOTTOM}; for(unsigned int i = 0; i < balls.size(); i++) { for(int j = 0; j < 6; j++) { BallWallPair bwp; bwp.ball = balls[i]; bwp.wall = walls[j]; potentialCollisions.push_back(bwp); } } */ }
In these function, we compute all possible ball-ball and ball-wall collisions, and add them to a C++ vector. They just ask the octree for the potential collisions. As I mentioned, we'll worry about how the octree works after we cover the basic mechanics of the program.
For those of you who are not familiar with the C++ vector, it's basically a variable-length array. To use it, you have to #include <vector>. You can add something to the end of a vector by calling vec.push_back(element). You can get or set the (n + 1)th element using vec[n], just like you would with an array. You can determine the number of elements in a vector by calling vec.size(). It can also do plenty of other things. (It slices, it dices, it does your homework and makes you breakfast.) And, to declare a vector of BallPairs, for example, we use vector<BallPair>.
Next, we have the moveBalls function, which moves all of the balls by their velocity times some float dt, in order to advance them by some small amount of time. Then, we have the applyGravity function, called every TIME_BETWEEN_UPDATES seconds. It applies gravity to the balls by decreasing the y coordinate of their velocities by GRAVITY * TIME_BETWEEN_UPDATES. That's similar to how gravity works in real life; it decreases an object's velocity in the y direction at a rate of 9.8 meters per second per second.
//Returns whether two balls are colliding bool testBallBallCollision(Ball* b1, Ball* b2) { //Check whether the balls are close enough float r = b1->r + b2->r; if ((b1->pos - b2->pos).magnitudeSquared() < r * r) { //Check whether the balls are moving toward each other Vec3f netVelocity = b1->v - b2->v; Vec3f displacement = b1->pos - b2->pos; return netVelocity.dot(displacement) < 0; } else return false; }
This function tests whether two balls are currently colliding. If (b1->pos - b2->pos).magnitudeSquared() < r * r is false, meaning they balls are farther away than the sum of their radii, then we know they're not colliding. Otherwise, we have to check whether the balls are moving towards each other or away from each other. If they're moving away from each other, then most likely they just collided, and they shouldn't "collide" again.
//Handles all ball-ball collisions void handleBallBallCollisions(vector<Ball*> &balls, Octree* octree) { vector<BallPair> bps; potentialBallBallCollisions(bps, balls, octree); for(unsigned int i = 0; i < bps.size(); i++) { BallPair bp = bps[i]; Ball* b1 = bp.ball1; Ball* b2 = bp.ball2; if (testBallBallCollision(b1, b2)) { //Make the balls reflect off of each other Vec3f displacement = (b1->pos - b2->pos).normalize(); b1->v -= 2 * displacement * b1->v.dot(displacement); b2->v -= 2 * displacement * b2->v.dot(displacement); } } }
handleBallBallCollisions makes all colliding balls bounce off of each other. First, we call potentialBallBallCollisions to find possible collisions. Then, we go through all of the potential collisions to find which ones are really collisions. For each one, we make the balls bounce off of each other, by reversing the velocity of each in the direction from the center of one ball to the other. The following picture illustrates how we compute the velocity of a ball after bouncing:
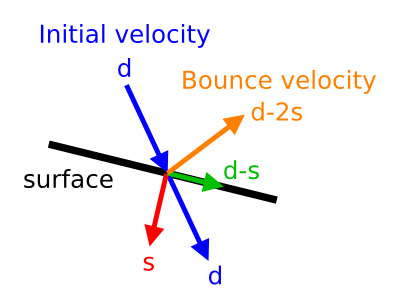
In the picture, d is the initial velocity of the ball. s is its projection onto the vector from the ball to the ball off which it's bouncing. d - 2s is the velocity of the ball after the bounce.
To determine s, we find the direction from the second ball to the first using (b1->pos - b2->pos).normalize(). Then, we take the dot product of the initial velocity and this direction, which gives s.
Since the balls don't slow down when they bounce, the balls will keep bouncing around forever, allowing for days or even years of non-stop entertainment.
Then, we have the testBallWallCollision function, which returns whether a particular ball is colliding with a given wall. Again, we have to check to make sure that the ball is moving toward the wall before we say that they're colliding.
//Handles all ball-wall collisions void handleBallWallCollisions(vector<Ball*> &balls, Octree* octree) { vector<BallWallPair> bwps; potentialBallWallCollisions(bwps, balls, octree); for(unsigned int i = 0; i < bwps.size(); i++) { BallWallPair bwp = bwps[i]; Ball* b = bwp.ball; Wall w = bwp.wall; if (testBallWallCollision(b, w)) { //Make the ball reflect off of the wall Vec3f dir = (wallDirection(w)).normalize(); b->v -= 2 * dir * b->v.dot(dir); } } }
Now, we have a function that makes all balls that are colliding with a wall bounce. Like in handleBallBallCollisions, we compute potential ball-wall collisions, go through them and find the actuall ball-wall collisions, and make the balls bounce. To bounce, we reverse the velocity of the ball in the direction perpendicular to the wall.
//Applies gravity and handles all collisions. Should be called every //TIME_BETWEEN_UPDATES seconds. void performUpdate(vector<Ball*> &balls, Octree* octree) { applyGravity(balls); handleBallBallCollisions(balls, octree); handleBallWallCollisions(balls, octree); }
Now, we lump together the applyGravity, handleBallBallCollisions, and handleBallWallCollisions into a performUpdate function, which is what we call every TIME_BETWEEN_UPDATES seconds.
Next is a advance function, which takes care of calling moveBalls, and calling performUpdate every TIME_BETWEEN_UPDATES seconds.
vector<Ball*> _balls; //All of the balls in play float _angle = 0.0f; //The camera angle Octree* _octree; //An octree with all af the balls //The amount of time until performUpdate should be called float _timeUntilUpdate = 0; GLuint _textureId;
Here are all of our global variables. Global variables are normally bad, because to understand a global variable, you potentially have to keep the whole main.cpp file in your head at once. Global variables are easily abused by altering them in ways that may confuse or subtly affect other functions. There are better approaches than global variables, but I won't use them here because I don't want to distract from collision detection. Instead, we'll pretend they're not global, and that they can only be accessed in the "toplevel functions" initRendering, drawScene, handleKeypress, handleResize, and a function we'll see called cleanup. To make them stand out, we'll have them all start with underscores. (By the way, in C++, you're not allowed to begin a variable with two underscores, or with one underscore followed by a capital letter.)
//Deletes everything. This should be called when exiting the program. void cleanup() { for(unsigned int i = 0; i < _balls.size(); i++) { delete _balls[i]; } delete _octree; }
When we exit the program, we need to make sure to delete all of the balls and the octree, since we don't need them any more.
void handleKeypress(unsigned char key, int x, int y) { switch (key) { case 27: //Escape key cleanup(); exit(0);
When the user presses ESC, we call cleanup and exit the program.
case ' ': //Add 20 balls with a random position, velocity, radius, and color for(int i = 0; i < 20; i++) { Ball* ball = new Ball(); ball->pos = Vec3f(8 * randomFloat() - 4, 8 * randomFloat() - 4, 8 * randomFloat() - 4); ball->v = Vec3f(8 * randomFloat() - 4, 8 * randomFloat() - 4, 8 * randomFloat() - 4); ball->r = 0.1f * randomFloat() + 0.1f; ball->color = Vec3f(0.6f * randomFloat() + 0.2f, 0.6f * randomFloat() + 0.2f, 0.6f * randomFloat() + 0.2f); _balls.push_back(ball); _octree->add(ball); } } }
When the user presses space bar, we make 20 balls with random positions, velocities, radii, and colors, and add them to the octree and the _balls vector.
If you look at drawScene, you'll see that we first draw the top and bottom of the box. Then, we draw the balls, using the following code:
//Draw the balls for(unsigned int i = 0; i < _balls.size(); i++) { Ball* ball = _balls[i]; glPushMatrix(); glTranslatef(ball->pos[0], ball->pos[1], ball->pos[2]); glColor3f(ball->color[0], ball->color[1], ball->color[2]); glutSolidSphere(ball->r, 12, 12); //Draw a sphere glPopMatrix(); }
We have a new function here, glutSolidSphere, which draws a sphere. The first parameter is the radius of the sphere. The second and third indicate the number of polygons we'll use to draw the sphere will have; the bigger the numbers, the more polygons we use and the better the sphere will look.
//Called every TIMER_MS milliseconds void update(int value) { advance(_balls, _octree, (float)TIMER_MS / 1000.0f, _timeUntilUpdate); _angle += (float)TIMER_MS / 100; if (_angle > 360) { _angle -= 360; } glutPostRedisplay(); glutTimerFunc(TIMER_MS, update, 0); }
Our update function just calls advance and increases the angle of rotation.
Octree Code
That does it for the basic mechanics; now let's see how our octree works.
const int MAX_OCTREE_DEPTH = 6; const int MIN_BALLS_PER_OCTREE = 3; const int MAX_BALLS_PER_OCTREE = 6;
These are the parameters of our octree. We want a maximum depth of 6. When the number of balls in a cube reaches 6, we want to divide it into smaller cubes. When it goes below 3, we want to un-divide it.
//Our data structure for making collision detection faster class Octree { private: Vec3f corner1; //(minX, minY, minZ) Vec3f corner2; //(maxX, maxY, maxZ) Vec3f center;//((minX + maxX) / 2, (minY + maxY) / 2, (minZ + maxZ) / 2)
We start with the fields in our Octree class. We have the corner1, which is the lower-left-far corner of the cube, corner2, which is the upper-right-near corner, and center, which is the middle of the cube.
/* The children of this, if this has any. children[0][*][*] are the
* children with x coordinates ranging from minX to centerX.
* children[1][*][*] are the children with x coordinates ranging from
* centerX to maxX. Similarly for the other two dimensions of the
* children array.
*/
Octree *children[2][2][2];Now, we have the children nodes of the octree, if there are any. The children would themselves be octrees. Read the comment above the field.
//Whether this has children bool hasChildren; //The balls in this, if this doesn't have any children set<Ball*> balls; //The depth of this in the tree int depth; //The number of balls in this, including those stored in its children int numBalls;
These fields are pretty self-explanatory. The balls variable is a C++ set. To use a set, we #include <set>. To add an element to it, we call s.insert(element). To remove an element, we call s.erase(element). We can remove all of the elements from a set using s.clear().
//Adds a ball to or removes a from one to the children of this void fileBall(Ball* ball, Vec3f pos, bool addBall) { //Figure out in which child(ren) the ball belongs for(int x = 0; x < 2; x++) { if (x == 0) { if (pos[0] - ball->r > center[0]) { continue; } } else if (pos[0] + ball->r < center[0]) { continue; } for(int y = 0; y < 2; y++) { if (y == 0) { if (pos[1] - ball->r > center[1]) { continue; } } else if (pos[1] + ball->r < center[1]) { continue; } for(int z = 0; z < 2; z++) { if (z == 0) { if (pos[2] - ball->r > center[2]) { continue; } } else if (pos[2] + ball->r < center[2]) { continue; } //Add or remove the ball if (addBall) { children[x][y][z]->add(ball); } else { children[x][y][z]->remove(ball, pos); } } } } }
The fileBall method finds out the children where a ball belongs, based on the position pos and either adds it to or removes it from those children, calling the add and remove methods that we'll see later. To make things easier, rather than check whether a given ball intersects each cube, we check whether the ball's bounding box intersects each cube. It's okay for a node to have extra balls like this.
//Creates children of this, and moves the balls in this to the children void haveChildren() { for(int x = 0; x < 2; x++) { float minX; float maxX; if (x == 0) { minX = corner1[0]; maxX = center[0]; } else { minX = center[0]; maxX = corner2[0]; } for(int y = 0; y < 2; y++) { float minY; float maxY; if (y == 0) { minY = corner1[1]; maxY = center[1]; } else { minY = center[1]; maxY = corner2[1]; } for(int z = 0; z < 2; z++) { float minZ; float maxZ; if (z == 0) { minZ = corner1[2]; maxZ = center[2]; } else { minZ = center[2]; maxZ = corner2[2]; } children[x][y][z] = new Octree(Vec3f(minX, minY, minZ), Vec3f(maxX, maxY, maxZ), depth + 1); } } } //Remove all balls from "balls" and add them to the new children for(set<Ball*>::iterator it = balls.begin(); it != balls.end(); it++) { Ball* ball = *it; fileBall(ball, ball->pos, true); } balls.clear(); hasChildren = true; }
The haveChildren method is what divides a cube into eight smaller cubes, whenever we need to do that. To make each child, we call new Octree(Vec3f(minX, minY, minZ), Vec3f(maxX, maxY, maxZ), depth + 1), using a constructor that we'll see later.
Next, we have the collectBalls method, which finds all of the balls in a node or one of its children. We'll need this for when we un-divide a cube.
//Destroys the children of this, and moves all balls in its descendants //to the "balls" set void destroyChildren() { //Move all balls in descendants of this to the "balls" set collectBalls(balls); for(int x = 0; x < 2; x++) { for(int y = 0; y < 2; y++) { for(int z = 0; z < 2; z++) { delete children[x][y][z]; } } } hasChildren = false; }
This is where we un-divide a cube.
//Removes the specified ball at the indicated position void remove(Ball* ball, Vec3f pos) { numBalls--; if (hasChildren && numBalls < MIN_BALLS_PER_OCTREE) { destroyChildren(); } if (hasChildren) { fileBall(ball, pos, false); } else { balls.erase(ball); } }
This removes a ball from the octree.
Before we move on, we should know how we identify potential ball-wall collisions. To find potential collisions with the left wall, we just find the nodes that are at the extreme left, and return all of those balls. We use the same idea for the other five walls.
/* Helper fuction for potentialBallWallCollisions(vector). Adds * potential ball-wall collisions to cs, where w is the type of wall, * coord is the relevant coordinate of the wall ('x', 'y', or 'z'), and * dir is 0 if the wall is in the negative direction and 1 if it is in * the positive direction. Assumes that this is in the extreme * direction of the coordinate, e.g. if w is WALL_TOP, the function * assumes that this is in the far upward direction. */ void potentialBallWallCollisions(vector<BallWallPair> &cs, Wall w, char coord, int dir) { if (hasChildren) { //Recursively call potentialBallWallCollisions on the correct //half of the children (e.g. if w is WALL_TOP, call it on //children above centerY) for(int dir2 = 0; dir2 < 2; dir2++) { for(int dir3 = 0; dir3 < 2; dir3++) { Octree *child; switch (coord) { case 'x': child = children[dir][dir2][dir3]; break; case 'y': child = children[dir2][dir][dir3]; break; case 'z': child = children[dir2][dir3][dir]; break; } child->potentialBallWallCollisions(cs, w, coord, dir); } } } else { //Add (ball, w) for all balls in this for(set<Ball*>::iterator it = balls.begin(); it != balls.end(); it++) { Ball *ball = *it; BallWallPair bwp; bwp.ball = ball; bwp.wall = w; cs.push_back(bwp); } } }
This is a helper function for computing potential ball-wall collisions. It's explained in the comments.
public: //Constructs a new Octree. c1 is (minX, minY, minZ), c2 is (maxX, maxY, //maxZ), and d is the depth, which starts at 1. Octree(Vec3f c1, Vec3f c2, int d) { corner1 = c1; corner2 = c2; center = (c1 + c2) / 2; depth = d; numBalls = 0; hasChildren = false; }
On to our public functions. First is the constructor, which takes the two corners of the cube and the depth of the node. It's pretty self-explanatory.
//Destructor ~Octree() { if (hasChildren) { destroyChildren(); } }
And now, the destructor, which is called when the node is deleted. It deletes the children if there are any.
//Adds a ball to this void add(Ball* ball) { numBalls++; if (!hasChildren && depth < MAX_OCTREE_DEPTH && numBalls > MAX_BALLS_PER_OCTREE) { haveChildren(); } if (hasChildren) { fileBall(ball, ball->pos, true); } else { balls.insert(ball); } }
The add method adds a new ball to the octree.
//Removes a ball from this void remove(Ball* ball) { remove(ball, ball->pos); }
The method for removing a ball just calls our other remove method, using the ball's current position.
//Changes the position of a ball in this from oldPos to ball->pos void ballMoved(Ball* ball, Vec3f oldPos) { remove(ball, oldPos); add(ball); }
This method is called whenever the ball moves from a position oldPos to ball->pos. To make our lives easier, we just remove the ball and then add it again. We could go through the trouble of figuring out exactly in which cubes the ball is now, but wasn't, and in which cubes the ball was, but isn't any more. But I bet this wouldn't speed things up too much anyway.
//Adds potential ball-ball collisions to the specified set void potentialBallBallCollisions(vector<BallPair> &collisions) { if (hasChildren) { for(int x = 0; x < 2; x++) { for(int y = 0; y < 2; y++) { for(int z = 0; z < 2; z++) { children[x][y][z]-> potentialBallBallCollisions(collisions); } } } } else { //Add all pairs (ball1, ball2) from balls for(set<Ball*>::iterator it = balls.begin(); it != balls.end(); it++) { Ball *ball1 = *it; for(set<Ball*>::iterator it2 = balls.begin(); it2 != balls.end(); it2++) { Ball *ball2 = *it2; //This test makes sure that we only add each pair once if (ball1 < ball2) { BallPair bp; bp.ball1 = ball1; bp.ball2 = ball2; collisions.push_back(bp); } } } } }
Here's the meat of the octree. In this method, we compute all potential ball-ball collisions and put them in the collisions vector. If there are children, we just ask them for their potential ball-ball collisions; otherwise, we just take every pair of balls.
To go through all of the balls in a set, we use a special C++ construction. To iterate through a set, we used the following form:
for(set<Type>::iterator it = s.begin(); it != s.end(); it++) { Type element = *it; //Do stuff with element //... }
That's just the way sets work in C++.
//Adds potential ball-wall collisions to the specified set void potentialBallWallCollisions(vector<BallWallPair> &collisions) { potentialBallWallCollisions(collisions, WALL_LEFT, 'x', 0); potentialBallWallCollisions(collisions, WALL_RIGHT, 'x', 1); potentialBallWallCollisions(collisions, WALL_BOTTOM, 'y', 0); potentialBallWallCollisions(collisions, WALL_TOP, 'y', 1); potentialBallWallCollisions(collisions, WALL_FAR, 'z', 0); potentialBallWallCollisions(collisions, WALL_NEAR, 'z', 1); }
In this method, we compute all potential ball-wall collisions by calling our helper function six times, once for each wall.
And that's how our octree works.
Now, let's make sure we didn't do all that work for nothing, that the octree did speed things up. Run the program, and keep pressing space bar to see how many balls you can add until things start to slow down. If your computer's too fast, you might want to slow down the program by decreasing TIME_BETWEEN_UPDATES. (If your computer's too slow, you could increase TIME_BETWEEN_UPDATES, but then it'll look pretty cruddy.)
Let's compare this with the naive approach, where we check every pair of balls. In potentialBallBallCollisions and potentialBallWallCollisions, comment out the fast versions and uncomment the slow versions. In moveBalls, comment out the line that says octree->ballMoved(ball, oldPos). In handleKeypress, comment out the line that says _octree->add(ball). Now, see how many balls you can add until the program starts to slow down. It's much fewer. On my computer, 300 balls without the octree are about as fast as 1000 balls with the octree. If we add the line cout << potentialCollisions.size() << '\n'; to the end of potentialBallBallCollisions, we see that if we use an octree, when there are 300 balls, the program checks an average of about 400 pairs of balls for collisions, much better than the roughly 50,000 we have to check if we use the naive approach.
So, yay! We sped up collision detection a lot.
Next is "Lesson 11: Putting It All Together".
- Summary
- *
- Text version
- *
- Exercises
- *
- Download source